PID控制器
可调参数可选 或者
分别为比例、积分、微分控制参数
ZN 整定
临界比例带法Ziegler-Nichols tuning method
可获得良好的干扰抑制,但未必获得良好的设定值响应性能
闭环控制下,令 ,将 从小开始往上调,直到在阶跃输入下达到临界稳定,产生幅值和周期不变的持续震荡,记录比例增益 为临界增益, 为临界振荡周期
按以下整定规则配制
| 控制器类型 | |||
|---|---|---|---|
| 比例控制 P | - | - | |
| 比例积分控制 PI | - | ||
| 比例微分控制 PD | - | ||
| 比例积分微分控制 PID |
与控制器的公式相像,比例是乘常数,积分是两者除,微分是两者乘
开环Ziegler-Nichols整定规则
| 控制器类型 | |||
|---|---|---|---|
| 比例控制P | - | - | |
| 比例积分控制PI | - | ||
| 比例积分微分控制PID |
使用条件,输出信号如下图所示: 为斜率, 是纯滞后时间
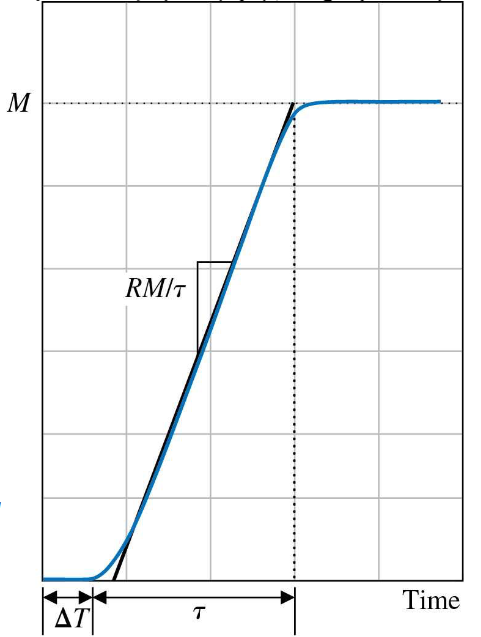
近似模型
λ整定
记忆
| 被控对象 | |||
|---|---|---|---|
| - | |||
| - | - | ||
| - |
根据闭环系统过渡过程时间 的要求,选择λ,满足
原理
期望传递函数具有以下形式
λ为设定的期望闭环系统时间常数,τ为纯滞后
考虑闭环系统传递函数:
简单变换后得到:
再对 进行运算(需要用到泰勒展开近似,此处不展开)
*手动整定法
据我们老师所说,每个人用的都不一样,且结论大多为经验总结,只可做参考,不能当作一般性结论
| 参数调整 | 百分比超调量 | 调整时间 | 稳态误差 |
|---|---|---|---|
| 增大 | 增大 | 影响很小 | 减小 |
| 增大 | 增大 | 增大 | 稳态误差为 0 |
| 增大 | 减小 | 减小 | 没有影响 |