频域稳定性

引论

Nyquist 稳定性判据，数学基础是复变函数的柯西定理 考虑闭环系统特征方程

$$F(s){=}1{+}L(s){=}0,\quad L(s){=}G_c(s)G(s)H(s)$$

稳定性判据： F(s) 的零点（也就是最终闭环传递函数的极点），需全部落到左半 S 平面 Nyquist 判据：将上述判据从 S 平面转移到 F(s) 平面，并得到相应的等效判据 开环传递函数之于闭环系统

映射围线

讲解使用的是 S 平面围线 → F (s) 平面围线，后续实际的是 S 平面围线 → L (s) 围线

Nyquist 判据

$L(s)$ 平面上的围线 $\Gamma_{L}$ 逆时针包围 $(-1,j0)$ 点的次数 $N$，等于开环系统环路传递函数 $L(s)$ 不稳定极点的个数 $P$ (其实是 $N=-P$，顺时针包围为正)

eg

两实极点系统

$$\begin{aligned}&L(s)=G_c(s)G(s)H(s)\\&L(s)=\frac K{\left(\tau_1s+1\right)\left(\tau_2s+1\right)}=\frac{100}{\left(s+1\right)\left(0.1s+1\right)}\end{aligned}$$$$K{=}100,\quad\tau_1{=}1,\quad\tau_2{=}0.1$$

简单计算列出表格

$$\boxed{\begin{array}{c|c|c|c|c|c|c|c|c|c|c}\omega&0&0.1&0.76&1&2&10&20&100&\infty\\\hline|L(j\omega)|&100&96&79.6&70.7&50.2&6.8&2.24&0.10&0\\\hline\angle L(j\omega)&0&-5.7&-41.5&-50.7&-74.7&-129.3&-150.5&-173.7&-180\\\end{array}}$$

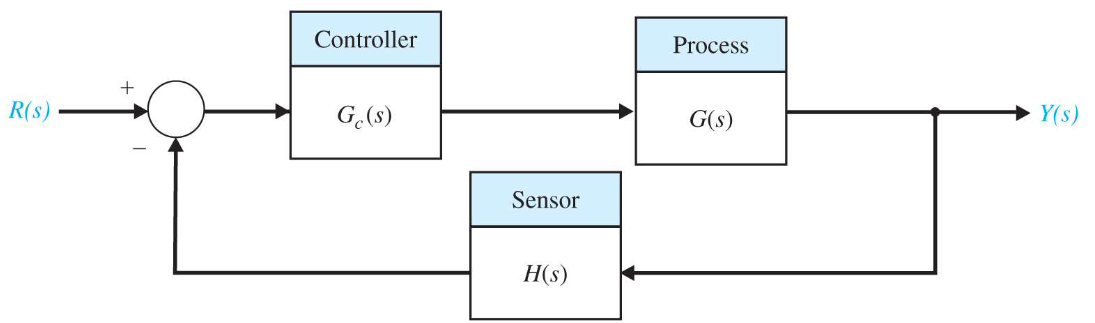
画出简图，由上表画出左图，再映射画出右图

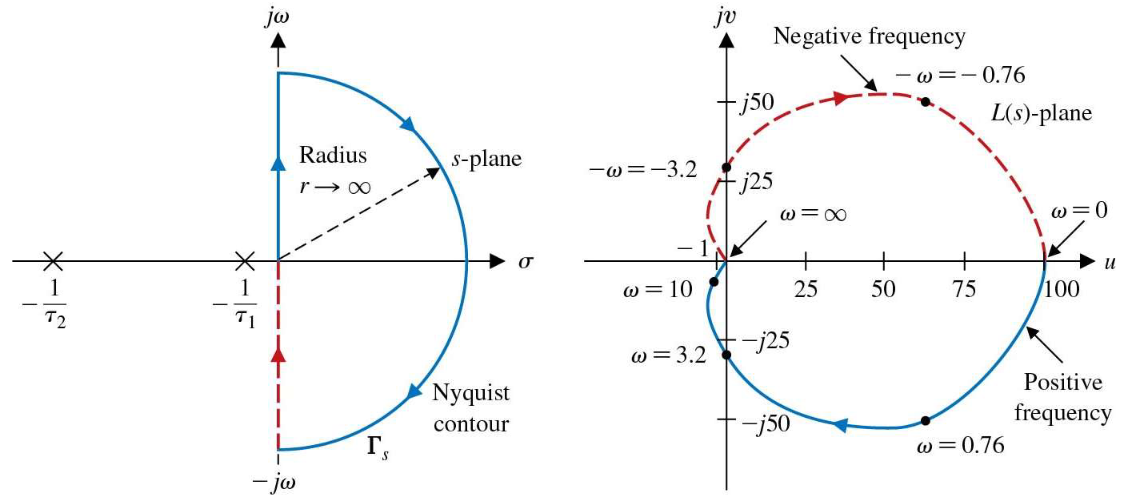
S平面上围线 $\Gamma_{S}$ 的正虚轴部分 $+j\omega$，映射为 $L(s)$ 平面上 Nyquist 图；负虚轴部分 $-j\omega$，映射到 $L(s)$ 平面与 Nyquist 图关于实轴对称（负频率特性）；半径为 $r \to \infty$ 的半圆周映射为 $L(s)$ 平面的原点。