复频域分析
Laplace 变换
s 具有时间的倒量纲,称为复频率
Laplace逆变换
根据拉普拉斯变换的定义可知,电流、电压象函数的单位分别为安秒(A・s)即库仑和伏秒(V・s)即韦伯
- 部分分式分解
- 基本变换对
复频域中的电路模型(运算电路)
电阻
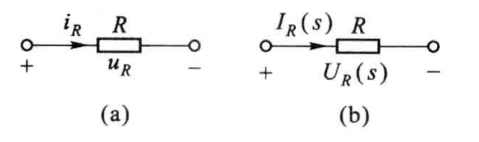
电容
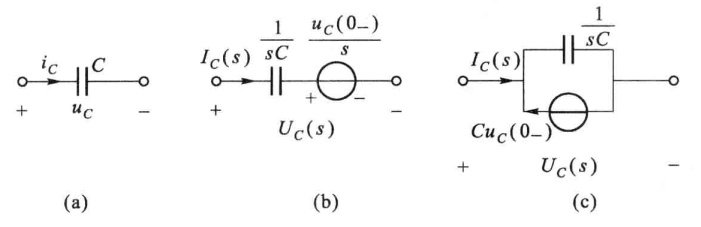
运算容抗: ,具有电阻的量纲
电感
运算感抗: ,具有电阻的量纲
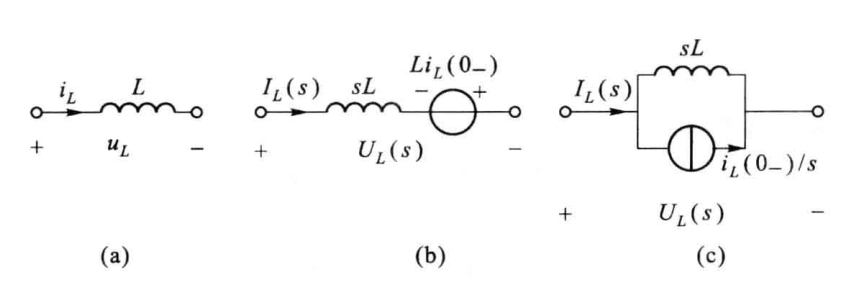
互感
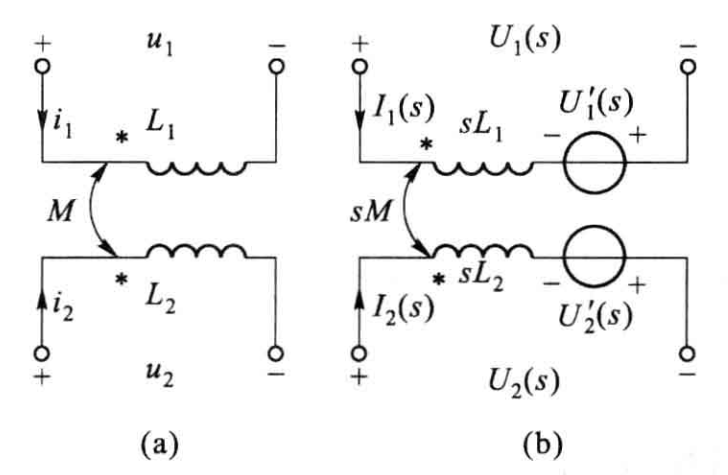
*辨析
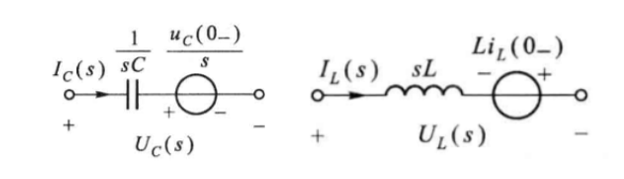
通常使用串联模型,电容的电压源提供能量,方向为+,电感的电压源吸收能量,方向为-,
运算电路
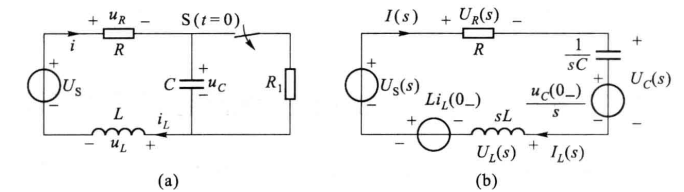
复频域欧姆定律
将电路中所有元件均用其复频域模型表示,所得电路模型称为原电路的复频域电路模型或运算电路(operational circuit)。
暂态过程分析步骤
- 元件处理:,激励源的象函数
- 运算电路搭建:组合元件,复频域阻抗+附加电源+电压电流象函数
- 求解:求出响应象函数
- 求反变换:部分分式展开,或积分变换