概率论第二章题目

5：推导两枚骰子点数之和的分布律（离散分布）。

2 → 7 和 12 → 7 分别对应 1 → 6 种情况

6：计算三枚骰子最大点数的分布律和数学期望。

$$X \sim \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ \frac{1}{216} & \frac{7}{216} & \frac{19}{216} & \frac{37}{216} & \frac{61}{216} & \frac{91}{216} \end{pmatrix}$$

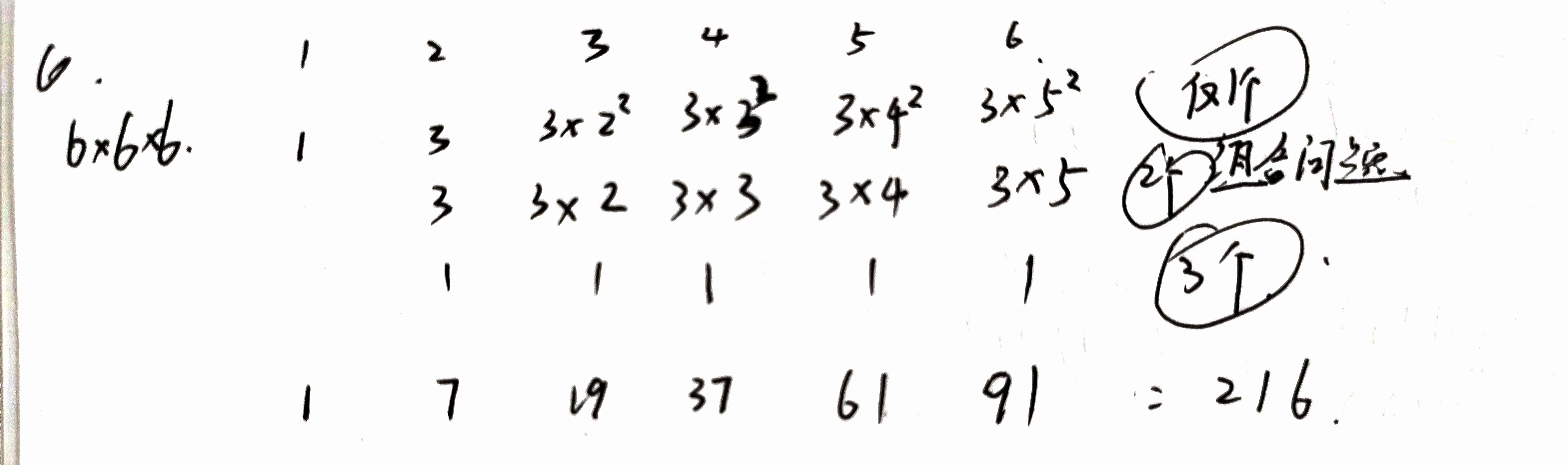
计算公式：设有 a 枚骰子，最大点数为 x，则 x 点对应的可能有 $\sum\limits_{i=1}^{a-1} a(x-1)^{a-i} + 1$

11：计算停止时间问题的分布律和累积分布函数（产品抽样）。

15：确定成功试验次数的分布（游戏关卡）。

注意是 4 次方，容易忽略成 2 次方

21：计算比赛中的概率（二项分布系列）。

这里第二题用 Bayes 公式更快，因为最终胜率都是 50%

30：计算彩票中奖概率和所需购买数量（二项分布）。

36：分析连续随机变量的分布函数（分段 CDF）。

43：分析连续随机变量的分布函数（指数分布）。

50：解决全国考研题目，涉及正态和均匀分布（概率密度）。

51：证明指数分布的充分必要条件（条件概率）。

58：计算随机变量的概率（泊松分布应用）。

65：求变换随机变量的密度函数（均匀分布变换）。

71：计算罐子中抽球的概率（动态抽样）。